Event Estimation Accuracy of Social Sensing With Facebook for Social Internet of Vehicles
- Kardelen Cepni, Mustafa Ozgur , Member, IEEE, and Ozgur B. Akan , Fellow, IEEE
1. introduction
SIoV란 인터넷을 통하여 차량끼리 연결을 제공하는 것이다. 보통 SIoV는 차량끼리의 통신을 말하지만 이 논문에서는 사람도 차량의 일부가 될 수 있다고 말하고 있다. 구체적으로는 사람이 제공하는 정보를 사용하는 것으로 소셜 네트워크를 사용하는 것을 말한다. 그래서 본 논문에서는 소셜 네트워크를 통해 차량에 탑승한 사람들의 관찰로부터 도로상의 사건들을 추정하는 것을 목표로 한다.
본 논문에서는 소셜 센싱이라는 단어가 많이 나오는데 소셜 센싱이란 물리적 현상 감지를 위한 OSN에서 공유되는 정보를 활용하는 것으로 여기서 OSN은 online social network의 줄임말이다. 그림과 같이 OSN에서 나온 데이터를 활용하여 수집하고 분석하는 것을 말한다. OSN을 활용하면 이벤트에 대한 집단 관찰에 대해 이해가 가능하며 이는 중요한 이벤트나 온라인 마케팅에서 적용할 때 중요하기 때문에, 소셜 센싱 메커니즘과 관찰의 정확도는 중요한 문제라고 할 수 있다.
또한 본 논문에서는 OSN 중에서 Facebook을 선정하여 연구를 진행하였으며, 그 이유는 2014년 에 제일 인기있는 OSN으로 선정되었으며 이제까지 facebook을 소셜 센싱 능력으로 진행한 연구가 없어서이다. 또한 facebook은 소셜 센싱의 매체의 기능을 나타내고 있다. 첫번째는 사용자가 친구들의 의견을 조사할 수 있도록 허락하는 Opinion Poll 플랫폼을 가지고 있다. 두번째는 Hashtag page 기능으로, 이 기능은 키워드로 데이터를 수집할 수 있음을 말한다. 세번째는 사용자의 공간을 통한 사용자들의 상호작용을 기반으로 하며, 이는 사용자들이 댓글을 달거나 좋아요를 누르는 행위를 말한다.
comment thread는 소셜 센싱 매체이며 예로 한 포스트에 댓글을 다는 행위를 들 수 있다. 이 때 댓글 하나가 하나의 comment thread가 되고, 이는 특별한 이벤트에 대해 사용자들의 의견을 수집할 수 있도록 하며 이 전체적인 의견 형성 과정 과정을 comment thread network 라고 하며 앞으로 CTN이라고 부른다. CTN을 사용한 소셜 감지는 주로 소셜 센서에서 비롯된 여러 요인으로 인해 기존 감지 방식과 근본적으로 다르다. 관찰 신호는 CTN을 통하여 사용자들로부터 발생되는데 이때 사용자의 인식으로 인한 노이즈 구성요소까지 포함되며, 다양한 형식의 관찰 신호가 공유되면서 추가적인 노이즈가 발생된다. 때문에 본 논문에서는 SIoV 도메인에서 다음을 적용하기 위해 조사한다.
2. preliminaries on facebook comment thread network
facebook을 통한 CTN의 소셜 센싱에서 사용자 관찰은 시간이 지남에 따라 발달하기 때문에 시퀀스 프로세스다. 모든 코멘트는 몇시간 만에 만들어지기 때문에 이 연구에서는 time window 제한을 두어야 한다. 그래서 본 논문에서는 time window를 참가한 사용자 수로 하며 comment는 time step별로 발생된다고 가정한다.

다음 그림은 과정을 보여주며 u0이 포스트를 게시하면 comment thread가 생기고 다음 시간에 u1이 comment를 생성하면 comment thread에 포함된다. 이렇게 각 사용자마다 포스트가 생기며 그 포스트의 집합은 다음과 같이 정리한다. 또한 각 포스트마다 받은 좋아요도 따로 집합으로 정리한다. 오른쪽 그림은 정리된 집합을 사용하여 이벤트에 대한 추정량을 구하는 과정이다.
본 논문에서는 comment와 like를 다음과 같이 정의한다. 먼저 comment는 주어진 사실을 기반으로 개인의 반응 또는 태도를 발언하는 것으로 Type은 다음과 같이 여러 개가 있으며 like는 주어진 의견에 지지를 표현하는 행동이라고 정의한다. 또한 모델은 불연속 시간 프레임워크를 사용하였으며, 고정된 시간별로 post가 생성된다고 가정하고 각 유저는 합리적은 사용자이기 때문에 거짓말을 하거나 불확실한 관찰을 공유하지 않는다고 가정한다.
3. comment thread network model
모델에 대한 설명은 다음과 같다. 커뮤니티에서 친구관계는 가중치 그래프로 구성되며 각 노드는 페이스북 사용자이다. 가중치 그래프는 인접행렬로 표현되며 커뮤니티 사이즈가 N+1일 때, 사이즈는 N+1 by N+1 이다. 각 값은 nonbinary value로 0에서 1사이의 값을 가지고 있으며 값이 높을수록 친밀한 관계다. 또한 모델에서의 세타는 이벤트가 어떤 것인지에 대해 영향을 많이 받는데 예를 들어 축구경기의 결과에 대한 모델이면 결과는 승 패로 나뉘기 때문에 binary signal이 되며 온도에 대한 모델이면 연속적인 값이 된다. 이 모델에서 중요한 부분은 참가한 사용자들로, 이 사용자들이 그들의 인식을 통하여 소셜 센서로써 역할을 한다. 그러나 사용자는 인식 및 관찰 결과를 코멘트 쓰레드에 반영하는 방법에서 발생하는 다양한 방법에서 노이즈를 도입할 수 있다. 그래서 사용자의 관찰 신호를 순수 관찰 신호와 관찰 인코딩 노이즈 두가지로 나누고 그것의 특징에 대해서 살펴본다.
먼저 순수 관찰 신호는 이벤트에 대한 사용자의 인식을 나타내는 신호다. 관찰값은 시간의 변화에 따라 인식이 변할 수 있기 때문에 정확히 세타로 표현할 수 없으며 평균은 세타이고 분산은 시그마 세타 제곱인 가우시안 랜덤변수를 사용한다.
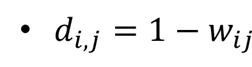
친구와의 거리를 구하는 식은 다음과 같으며 친구 관계가 강할수록 적은 값이 나온다. 이 식을 사용하여 사용자 i와 j간의 확률적인 관계를 가정한다.

i의 관찰 값과 j의 관찰값의 상관관계식은 다음과 같으며, 여기서 x와 y는 각 post의 시간을 나타내고 공분산은 게시물 사이의 우정 및 시간 거리에 대한 사용자 관찰 사이의 상관관계를 정의하기 때문에 공분산을 사용하여 계산합니다.

다변량 지수 공분산 함수는 다음과 같다. 여기서 θF & θT 는 상관계수이며 우정 및 시간 거리와 관련하여 공분산이 얼마나 빨리 떨어지는지 결정한다. 또한 f는 관찰된 이벤트에 대한 샘플링 속도로 얼마나 자주 post가 생성되는지를 나타낸다. 본 논문에서는 포스트가 불연속 시간 프레임워크를 통해 매 분마다 발생된다고 가정하기 때문에 f의 비율은 하나의 샘플 당 1분으로 가정한다.
두번째 신호인 관찰 인코딩 노이즈에 대한 설명이다. 알다시피 페이스북 형식에는 다양한 형식이 존재하는데 이로 인해 순수 관찰 신호가 형식에 따라 다르게 묘사될 수 있다. 또한 사용자가 다르게 인식 및 학습을 할 수 있기 때문에 포스트 타입에 근거하여 사용자의 관찰에 추가적인 노이즈를 도입함으로써 다른 포스트 타입의 효과를 통합한다. 이러한 노이즈를 관찰 인코딩 노이즈라고 한다.
본 논문에서는 포스트 타입을 텍스트와 링크 타입 두가지로 제한하여 분석한다. 또한 텍스트 기반 포스트가 링크 기반 포스트보다 신뢰성이 낮다고 가정한다.



그러면 전체적인 관찰신호에 대한 값은 다음과 같이 계산된다. 여기서 a는 텍스트 기반 포스트를 말하고 b는 링크 기반 포스트이다. 각각은 binary value로 0또는 1의 값을 가지며, v함수는 관찰 인코딩 노이즈 값이며 가우시안 랜덤변수이다. 텍스트 기반 포스트가 신뢰성이 더 낮다고 가정했기 때문에 텍스트에 대한 분산값이 더 크도록 가정한다.
다음은 코멘트와 좋아요에 대하여 설명이다. post0의 관찰 신호 값은 so로 나타낼 수 있고 post1의 관찰 신호 값은 post0의 관찰 신호 값에 post1관찰 신호 값을 더한 것이라고 할 수 있다. 사용자는 각 의견에 가중치를 할당하여 관찰 내용을 업데이트한다. 가중치는 이전의 포스트에서 할당받으므로 사용자간 우정관계를 가중치로 사용한다. 그러면 식은 다음과 같이 정리되고 모든 post 집합에 대한 관찰 신호 값은 다음과 같이 정리할 수 있다.

또한 좋아요는 의견 공유의 호감도를 나타내며 몇가지 요인에 의존한다. 첫번째는 만약 post A가 post B보다 먼저 생겼다면 좋아요 개수는 A가 더 많을 것이다. 두번째는 커뮤니티 안에서 다른 사람보다 더 인기있는 사람이라면 좋아요를 더 받을 것이다. 그러므로 좋아요는 다음과 같이 정리할 수 있다. x는 포스트의 존재시간을 나타내며 k는 이 포스트를 좋아하는 사용자 수이다. f는 이 포스트를 사용자가 좋아할 확률로 포스트의 내용보다는 한 커뮤니티 내에서의 관계강도를 반영한다. 즉 다른 사용자에 비해 f값이 높을수록 사용자가 커뮤니티에서 더 유리한 사용자임을 의미한다.
관측 신호에 대한 추정량은 다음과 같이 계산한다. 좋아요 개수의 합 분의 좋아요 개수 * 각 관측 신호 값으로 정리하면 다음과 같다.

페이스북 CTN의 소셜 센싱 능력을 평가하기 위하여 추정오차를 사용하였으며, 추정오차의 식은 다음과 같다.

4. numerical analysis
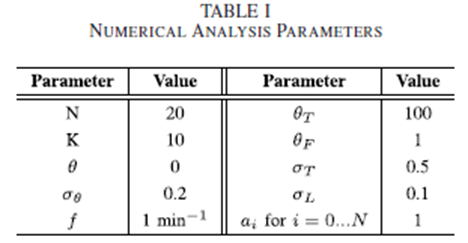
수치분석을 추정오차를 통하여 수행했으며 규모가 작은 커뮤니티에 초점을 맞추어 분석했다. 커뮤니티 안에서 관계를 모델링하는 동안에 랜덤 가중치 그래프를 사용하였으며 커뮤니티 안에서의 모든 사용자는 친구라고 가정한다. 또한 앞으로 보실 분석에서의 각 파라미터 값은 언급이 없으면 표 1에 정리되어 있는것과 같다.

먼저 네트워크 사이즈와 포스트 특성이 미치는 영향에 대한 분석 결과이다. 가로축은 comment thread의 개수이고 세로축은 추정 오차를 나타낸다. 분산이 크면 코멘트 개수가 많아져도 오차가 줄어들지 않는 반면 분산이 작을경우 개수가 많아질수록 오차가 작아지는 것을 볼 수 있다. 이는 CTN이 사용자 관찰 신호가 매우 변덕스러운 경우 모든 이벤트 유형에 대해 소셜 센싱에 적합하지 않을 수 있음을 나타낸다.

다음은 포스트 타입에 대한 정확도 검사이다. x축은 텍스트 데이터의 비율을 나타내며 텍스트 데이터가 많아질수록 오차율도 높아지는 것을 확인하였다. 정확히 0%에서 100%까지의 오차 비율은 5배가 올랐으며 이는 텍스트 데이터만 사용했을 때 소셜 센싱의 공감대를 불리하게 변화시킬 가능성이 있다는 것을 알 수 있다.

이번에는 사용자의 행동과 관계에 대하여 분석한 결과이다. 사용자들이 호감도가 동등하다는 가정으로 분석하였을 때 텍스트 데이터가 증가되더라도 추정오차는 많이 다르지 않았으며, 호감도를 반영한다는 것은 더 나은 성능을 제공하는 것을 알 수 있다.

다음은 가중치의 효과를 분석한 결과이다. 먼저 종종 자신의 관찰에 더욱 높은 가중치를 할당하는 사용자가 있는데 이를 자기 중심적인 코멘트라고 지칭한다. 자기 중심적일 때와 동등한 관계와 관계를 반영한 가중치 세가지를 비교하였을 때 친구 관계를 반영한 결과는 소수의 인기있는 개인의 관찰에 집중하게 됨으로써 더 많은 오류를 초래할 수 있음을 나타낸다.

다음은 사용자 간의 관계를 통한 분석 결과이다. 상관관계의 값이 증가할수록 추정 오차 값이 증가함을 확인하였으며 이는 상관관계가 적은 관찰은 소셜 센싱의 정확성에 유익하며 상관관계가 높으면 소셜 컨센선스를 편향시킬 가능성이 있음을 알 수 있다. 따라서 커뮤니티의 선정은 페이스북 CTN과 함께 소셜 센싱에 중요한 요소가 될 수 있다.
5. conclusion
CTN은 페이스북을 통한 소셜 센싱에서 중요한 메커니즘으로 관측치의 편중 가중치와 CTN에서 신뢰도가 낮은 포스트 타입의 사용은 추정 신호의 정확도를 악화시킨다. 커뮤니티 내의 사용자 관계에 따라 소셜 센싱의 신뢰성이 변화할 가능성이 있으며, 정확한 평가를 얻기 위해서는 소셜 센싱에서 OSN 유저의 선택이 불가결하다는 것이 시사된다. 향후 연구에서는 다양한 유형의 이벤트에 대하여 분석할 것이며 거짓말하는 사용자가 미치는 영향을 조사하고 이해하는 것을 목표로 할 것이며, 또한 모델을 향상시키기 위하여 더 많은 선택사항을 고려한다고 한다.
'PAPER' 카테고리의 다른 글
| 빅데이터처리 (0) | 2020.11.30 |
|---|---|
| 데이터구조(자료구조) (0) | 2020.11.30 |
| StoryLine-Unsupervised Geo-event Demultiplexing in Social Spaces without Location Information(2017) (0) | 2020.11.27 |
| 스마트차량과 자동차 사물인터넷(IoV) 기술동향 분석 (0) | 2020.10.12 |
| Pregel-A System for Large-Scale Graph Processing(2010) (0) | 2020.06.19 |



